k-means clustering with ruby

Sun May 2014

Let's say we have a collection of businesses in three distinct regions: the East coast, West coast and fly-over country, and we would like to classify these businesses by region. Clustering algorithms, which aim to partition a set of data points into a small number of clusters, are some of the most commonly used solutions for data classification problems.

The k-means algorithm is what we will use to cluster our data. It is an unsupervised machine learning algorithm that groups data points into k clusters, minimizing the distance from each data point to the centroid of the cluster it belongs to.

The Algorithm

Choose k points to represent the initial centroids for the data. These may be assigned randomly or specified by the user.
Assign each data point to the closest centroid (by euclidean distance or other distance metric), creating k clusters.
Recalculate each centroid's position such that each data point in the centroid's cluster is equidistant to the centroid.
Repeat steps 2 and 3 until convergence (no data points change cluster) or up to a maximum number of iterations.

The Code

Let's start by implementing classes to store the businesses, centroids and clusters. The DataPoint class will represent the businesses and centroids. A DataPoint should be able to do the following:

Store the latitude, longitude and state belonging to a business.
Calculate the distance between itself and another point or centroid.

Since we are dealing with geographical coordinates, for this implementation I've elected to use the geographic distance between points instead of the euclidean distance, using utilities from the Geocoder library. I would like to pass instances of the DataPoint class to the Geocoder library for distance calculations, so we will also need to implement an instance method, to_coordinates, that returns an array of latitude and longitude.

To store the data points, we will use a Set because it will make cluster comparison easier (for step 4 of the algorithm). The Ruby Set class uses the eql? and hash methods for equality comparisons, so our DataPoint class will also need to implement them.

Now that we have the basic gist of the requirements for the DataPoint class, let's write a few test cases to assert them.

subject { Algorithms::KMeans::DataPoint }
let(:args) { { latitude: -23.03, longitude: -77.25 } }
let(:args2) { { latitude: -33.03, longitude: -77.25 } }
 
context '#initialize' do
  it 'raises an error if initialized without latitude or longitude' do
    expect { subject.new(foo: 'bar') }.to raise_error(ArgumentError)
  end
 
  it 'does not raise an error if initialized with latitude and longitude' do
    expect { subject.new(args) }.not_to raise_error
  end
end
 
context '#geographic_distance' do
  it 'calculates the geographic distance between the same datapoint as zero' do
    expect(subject.new(args).geographic_distance(subject.new(args))).to eq(0)
  end
 
  it 'calculates the geographic distance between two datapoints' do
    expect(subject.new(args).geographic_distance(subject.new(args2))).to be > 500
  end
end
 
context 'external dependencies' do
  it 'implements geocoder methods' do
    expect(subject.new(args)).to respond_to(:to_coordinates)
  end
 
  it 'implements set comparison methods' do
    expect(subject.new(args)).to respond_to(:eql?, :hash)
  end
end

subject { Algorithms::KMeans::DataPoint }
let(:args) { { latitude: -23.03, longitude: -77.25 } }
let(:args2) { { latitude: -33.03, longitude: -77.25 } }
 
context '#initialize' do
  it 'raises an error if initialized without latitude or longitude' do
    expect { subject.new(foo: 'bar') }.to raise_error(ArgumentError)
  end
 
  it 'does not raise an error if initialized with latitude and longitude' do
    expect { subject.new(args) }.not_to raise_error
  end
end
 
context '#geographic_distance' do
  it 'calculates the geographic distance between the same datapoint as zero' do
    expect(subject.new(args).geographic_distance(subject.new(args))).to eq(0)
  end
 
  it 'calculates the geographic distance between two datapoints' do
    expect(subject.new(args).geographic_distance(subject.new(args2))).to be > 500
  end
end
 
context 'external dependencies' do
  it 'implements geocoder methods' do
    expect(subject.new(args)).to respond_to(:to_coordinates)
  end
 
  it 'implements set comparison methods' do
    expect(subject.new(args)).to respond_to(:eql?, :hash)
  end
end

The class implementation is pretty simple.

class DataPoint
  attr_reader :latitude, :longitude, :state
 
  def initialize(options)
    raise ArgumentError,  "Please initialize with :latitude, :longitude"
      if options[:latitude].nil? || options[:longitude].nil?
    @latitude = options[:latitude].to_f
    @longitude = options[:longitude].to_f
    @state = options[:state]
  end
 
  def geographic_distance(business)
    Geocoder::Calculations.distance_between(self, business)
  end
 
  # Geocoder dependency
  def to_coordinates
    [latitude, longitude]
  end
 
  # Set equality dependencies
  def eql?(other_object)
    latitude == other_object.latitude && longitude == other_object.longitude
  end
 
  def hash
    [latitude, longitude].hash
  end
end

class DataPoint
  attr_reader :latitude, :longitude, :state
 
  def initialize(options)
    raise ArgumentError,  "Please initialize with :latitude, :longitude"
      if options[:latitude].nil? || options[:longitude].nil?
    @latitude = options[:latitude].to_f
    @longitude = options[:longitude].to_f
    @state = options[:state]
  end
 
  def geographic_distance(business)
    Geocoder::Calculations.distance_between(self, business)
  end
 
  # Geocoder dependency
  def to_coordinates
    [latitude, longitude]
  end
 
  # Set equality dependencies
  def eql?(other_object)
    latitude == other_object.latitude && longitude == other_object.longitude
  end
 
  def hash
    [latitude, longitude].hash
  end
end

Up next is the Cluster class, which we will use to perform the following functions:

Store a centroid and a set of data points.
Recalculate the position of the centroid to make it equidistant to all points in the cluster within a very small margin of error.
Implement a method to compare itself with another cluster.

With these specifications in mind, we write the tests:

subject { Algorithms::KMeans::Cluster.new(data_points: [data_point1, data_point2]) }
let(:data_point1) { Algorithms::KMeans::DataPoint.new(latitude: -23.03, longitude: -77.25) }
let(:data_point2) { Algorithms::KMeans::DataPoint.new(latitude: -33.03, longitude: -77.25) }
let(:margin_of_error) { 0.00189394 } #10 ft
 
describe '#recompute_centroid!' do
  it 'sets the centroid to the geographic center of the cluster (within 10ft)' do
    subject.recompute_centroid!
    new_centroid = subject.centroid
    expect(data_point1.geographic_distance(new_centroid))
      .to be_within(margin_of_error)
      .of(data_point2.geographic_distance(new_centroid))
  end
end
 
describe '#clear!' do
  it 'removes all the data points' do
    subject.clear!
    expect(subject.data_points).to be_empty
  end
end
 
describe '#add_datapoint' do
  it 'adds a data point' do
    new_data_point = Algorithms::KMeans::DataPoint.new(latitude: -32.32, longitude: 78.2)
    expect { subject.add_datapoint(new_data_point) }
       .to change { subject.data_points.size }.by(1)
  end
end
 
describe '#==' do
  it 'returns true if two clusters have the same data points (order is irrelevant)' do
    cluster2 = Algorithms::KMeans::Cluster.new(data_points: [data_point2.dup, data_point1.dup])
    expect(cluster2).to be == subject
  end
end

subject { Algorithms::KMeans::Cluster.new(data_points: [data_point1, data_point2]) }
let(:data_point1) { Algorithms::KMeans::DataPoint.new(latitude: -23.03, longitude: -77.25) }
let(:data_point2) { Algorithms::KMeans::DataPoint.new(latitude: -33.03, longitude: -77.25) }
let(:margin_of_error) { 0.00189394 } #10 ft
 
describe '#recompute_centroid!' do
  it 'sets the centroid to the geographic center of the cluster (within 10ft)' do
    subject.recompute_centroid!
    new_centroid = subject.centroid
    expect(data_point1.geographic_distance(new_centroid))
      .to be_within(margin_of_error)
      .of(data_point2.geographic_distance(new_centroid))
  end
end
 
describe '#clear!' do
  it 'removes all the data points' do
    subject.clear!
    expect(subject.data_points).to be_empty
  end
end
 
describe '#add_datapoint' do
  it 'adds a data point' do
    new_data_point = Algorithms::KMeans::DataPoint.new(latitude: -32.32, longitude: 78.2)
    expect { subject.add_datapoint(new_data_point) }
       .to change { subject.data_points.size }.by(1)
  end
end
 
describe '#==' do
  it 'returns true if two clusters have the same data points (order is irrelevant)' do
    cluster2 = Algorithms::KMeans::Cluster.new(data_points: [data_point2.dup, data_point1.dup])
    expect(cluster2).to be == subject
  end
end

Followed by the class implementation:

class Cluster
  require 'geocoder'
 
  attr_reader :data_points, :centroid
 
  def initialize(options)
    options = defaults.merge(options)
    @data_points = Set.new(options[:data_points])
    @centroid = options[:centroid]
  end
 
  def recompute_centroid!
    lat, lng = Geocoder::Calculations.geographic_center(data_points)
    @centroid = DataPoint.new(latitude: lat, longitude: lng)
  end
 
  def add_datapoint(data_point)
    data_points.add(data_point)
  end
 
  def clear!
    data_points.clear
  end
 
  def ==(other_object)
    @data_points == other_object.data_points
  end
 
  private
 
  def defaults
    { data_points: Set.new }
  end
end

class Cluster
  require 'geocoder'
 
  attr_reader :data_points, :centroid
 
  def initialize(options)
    options = defaults.merge(options)
    @data_points = Set.new(options[:data_points])
    @centroid = options[:centroid]
  end
 
  def recompute_centroid!
    lat, lng = Geocoder::Calculations.geographic_center(data_points)
    @centroid = DataPoint.new(latitude: lat, longitude: lng)
  end
 
  def add_datapoint(data_point)
    data_points.add(data_point)
  end
 
  def clear!
    data_points.clear
  end
 
  def ==(other_object)
    @data_points == other_object.data_points
  end
 
  private
 
  def defaults
    { data_points: Set.new }
  end
end

Finally, we implement the algorithm in a class called Clusterer. This class needs to run through the four steps of the algorithm and terminate on convergence or after a maximum number of iterations. It should also export the clustered data in a format that we can plot on a map. Let's assert these requirements.

let(:filename)  { "#{File.dirname(__FILE__)}/../../../fixtures/k_means/data.json" }
subject { Algorithms::KMeans::Clusterer.new(filename: filename) }
let(:east_states) { %w(NY NJ PA MA VA) }
let(:west_states) { %w(CA NV OR WA) }
let(:fly_over_states) { %w(IA MO NE OK SD) }
let(:clusters) do
  lat_lngs = [
    { latitude: 37.757717, longitude: -122.410499 }, # San Francisco, CA
    { latitude: 40.764684, longitude: -73.988990 }, # Manhattan, NY
    { latitude: 42.137687, longitude: -100.178348}, # Goose Creek, NE
  ]
  lat_lngs.collect do |ll|
     Algorithms::KMeans::Cluster.new(centroid: Algorithms::KMeans::DataPoint.new(ll))
  end
end
 
describe '#run' do
  context 'with pre-determined clusters' do
    it 'clusters the data into east, west and flyover states' do
      subject.clusters = clusters
      subject.run
      states_by_cluster = subject.clusters.map {|s| s.data_points.classify(&:state).keys.to_set }.to_set
      expect(states_by_cluster)
         .to eq(Set.new([east_states.to_set, west_states.to_set, fly_over_states.to_set]))
    end
  end
 
  context 'without pre-determined clusters' do
    it 'divides the data into distinct clusters' do
      subject.run
      expect(subject.clusters.map { |cluster| cluster.data_points.size }.inject(:+))
         .to eq(subject.data_points.to_set.size)
    end
  end
end
 
describe '#to_chart_data' do
  it 'returns an array of data points grouped by cluster' do
    subject.clusters = clusters
    subject.run
    expect(subject.to_chart_data.group_by(&:last).size).to eq(3)
  end
end

let(:filename)  { "#{File.dirname(__FILE__)}/../../../fixtures/k_means/data.json" }
subject { Algorithms::KMeans::Clusterer.new(filename: filename) }
let(:east_states) { %w(NY NJ PA MA VA) }
let(:west_states) { %w(CA NV OR WA) }
let(:fly_over_states) { %w(IA MO NE OK SD) }
let(:clusters) do
  lat_lngs = [
    { latitude: 37.757717, longitude: -122.410499 }, # San Francisco, CA
    { latitude: 40.764684, longitude: -73.988990 }, # Manhattan, NY
    { latitude: 42.137687, longitude: -100.178348}, # Goose Creek, NE
  ]
  lat_lngs.collect do |ll|
     Algorithms::KMeans::Cluster.new(centroid: Algorithms::KMeans::DataPoint.new(ll))
  end
end
 
describe '#run' do
  context 'with pre-determined clusters' do
    it 'clusters the data into east, west and flyover states' do
      subject.clusters = clusters
      subject.run
      states_by_cluster = subject.clusters.map {|s| s.data_points.classify(&:state).keys.to_set }.to_set
      expect(states_by_cluster)
         .to eq(Set.new([east_states.to_set, west_states.to_set, fly_over_states.to_set]))
    end
  end
 
  context 'without pre-determined clusters' do
    it 'divides the data into distinct clusters' do
      subject.run
      expect(subject.clusters.map { |cluster| cluster.data_points.size }.inject(:+))
         .to eq(subject.data_points.to_set.size)
    end
  end
end
 
describe '#to_chart_data' do
  it 'returns an array of data points grouped by cluster' do
    subject.clusters = clusters
    subject.run
    expect(subject.to_chart_data.group_by(&:last).size).to eq(3)
  end
end

Here's an abridged version of the algorithm's implementation, showcasing the meat of the algorithm, which is pretty straightforward. The full Clusterer class is here.

class Clusterer
  MAX_ITERATIONS = 100
 
  def run
    load_data_points
    compute_initial_centroids if clusters.empty?
    MAX_ITERATIONS.times do
      clear_clusters
      assign_points_to_nearest_cluster
      old_clusters = Marshal.load(Marshal.dump(clusters))
      recompute_centroids
      assign_points_to_nearest_cluster
      clusters_did_not_change = old_clusters.zip(clusters).collect {|c1, c2| c1 == c2 }
      break unless clusters_did_not_change.include?(false)
    end
  end
end

class Clusterer
  MAX_ITERATIONS = 100
 
  def run
    load_data_points
    compute_initial_centroids if clusters.empty?
    MAX_ITERATIONS.times do
      clear_clusters
      assign_points_to_nearest_cluster
      old_clusters = Marshal.load(Marshal.dump(clusters))
      recompute_centroids
      assign_points_to_nearest_cluster
      clusters_did_not_change = old_clusters.zip(clusters).collect {|c1, c2| c1 == c2 }
      break unless clusters_did_not_change.include?(false)
    end
  end
end

Results

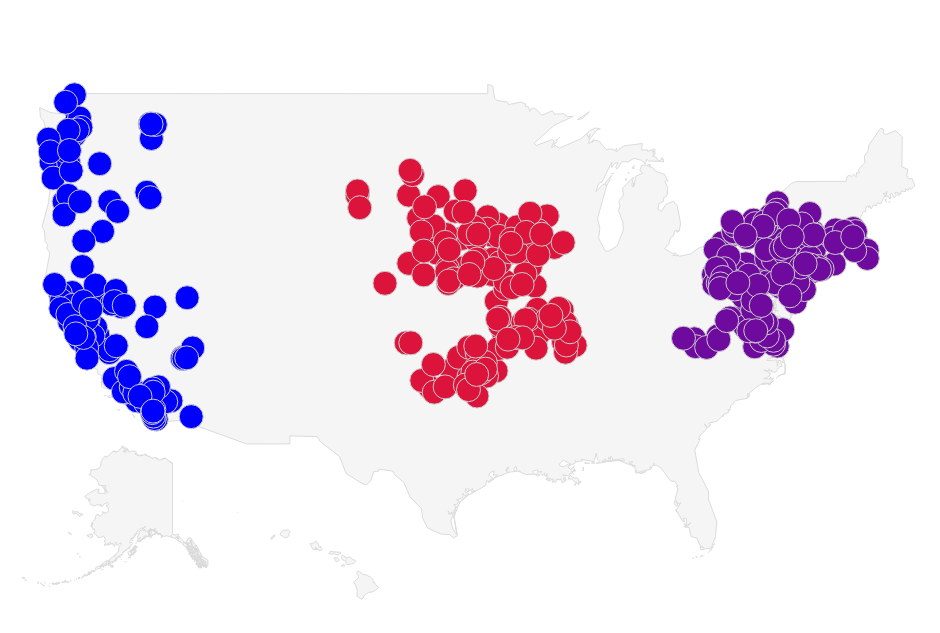
Since the k-means algorithm does not guarantee to find the global optimum, we can't expect that the data will be clustered in the same way after each run. However, given that we have some knowledge of the data we are clustering, we can provide initial centroids that will result in the global optimum. For the chart below I picked 500 businesses in groupings of states to make the clustering easier. I also chose the initial centroids to ensure that the algorithm found the global optimum. I plotted the chart using a Google Visualization.

k-means result

You can find the complete code for this blog post in my algorithms repository on github.