k-means clustering with ruby
Let's say we have a collection of businesses in three distinct regions: the East coast, West coast and fly-over country, and we would like to classify these businesses by region. Clustering algorithms, which aim to partition a set of data points into a small number of clusters, are some of the most commonly used solutions for data classification problems.
The k-means algorithm is what we will use to cluster our data. It is an unsupervised machine learning algorithm that groups data points into k clusters, minimizing the distance from each data point to the centroid of the cluster it belongs to.
The Algorithm
- Choose k points to represent the initial centroids for the data. These may be assigned randomly or specified by the user.
- Assign each data point to the closest centroid (by euclidean distance or other distance metric), creating k clusters.
- Recalculate each centroid's position such that each data point in the centroid's cluster is equidistant to the centroid.
- Repeat steps 2 and 3 until convergence (no data points change cluster) or up to a maximum number of iterations.
The Code
Let's start by implementing classes to store the businesses, centroids and clusters.
The DataPoint class will represent the businesses and centroids. A
DataPoint should be able to do the following:
- Store the latitude, longitude and state belonging to a business.
- Calculate the distance between itself and another point or centroid.
Since we are dealing with geographical coordinates, for this
implementation I've elected to use the geographic distance between
points instead of the euclidean distance, using utilities from the Geocoder library. I would like to pass instances of the DataPoint class to the Geocoder library for distance calculations, so we will also need to implement an instance method, to_coordinates, that returns an array of latitude and longitude.
To store the data points, we will use a Set because it will make cluster comparison easier (for step 4 of the algorithm). The Ruby Set class uses the eql? and hash methods for equality comparisons, so our DataPoint class will also need to implement them.
Now that we have the basic gist of the requirements for the DataPoint class, let's write a few test cases to assert them.
subject { Algorithms::KMeans::DataPoint }
let(:args) { { latitude: -23.03, longitude: -77.25 } }
let(:args2) { { latitude: -33.03, longitude: -77.25 } }
context '#initialize' do
it 'raises an error if initialized without latitude or longitude' do
expect { subject.new(foo: 'bar') }.to raise_error(ArgumentError)
end
it 'does not raise an error if initialized with latitude and longitude' do
expect { subject.new(args) }.not_to raise_error
end
end
context '#geographic_distance' do
it 'calculates the geographic distance between the same datapoint as zero' do
expect(subject.new(args).geographic_distance(subject.new(args))).to eq(0)
end
it 'calculates the geographic distance between two datapoints' do
expect(subject.new(args).geographic_distance(subject.new(args2))).to be > 500
end
end
context 'external dependencies' do
it 'implements geocoder methods' do
expect(subject.new(args)).to respond_to(:to_coordinates)
end
it 'implements set comparison methods' do
expect(subject.new(args)).to respond_to(:eql?, :hash)
end
endsubject { Algorithms::KMeans::DataPoint }
let(:args) { { latitude: -23.03, longitude: -77.25 } }
let(:args2) { { latitude: -33.03, longitude: -77.25 } }
context '#initialize' do
it 'raises an error if initialized without latitude or longitude' do
expect { subject.new(foo: 'bar') }.to raise_error(ArgumentError)
end
it 'does not raise an error if initialized with latitude and longitude' do
expect { subject.new(args) }.not_to raise_error
end
end
context '#geographic_distance' do
it 'calculates the geographic distance between the same datapoint as zero' do
expect(subject.new(args).geographic_distance(subject.new(args))).to eq(0)
end
it 'calculates the geographic distance between two datapoints' do
expect(subject.new(args).geographic_distance(subject.new(args2))).to be > 500
end
end
context 'external dependencies' do
it 'implements geocoder methods' do
expect(subject.new(args)).to respond_to(:to_coordinates)
end
it 'implements set comparison methods' do
expect(subject.new(args)).to respond_to(:eql?, :hash)
end
endThe class implementation is pretty simple.
class DataPoint
attr_reader :latitude, :longitude, :state
def initialize(options)
raise ArgumentError, "Please initialize with :latitude, :longitude"
if options[:latitude].nil? || options[:longitude].nil?
@latitude = options[:latitude].to_f
@longitude = options[:longitude].to_f
@state = options[:state]
end
def geographic_distance(business)
Geocoder::Calculations.distance_between(self, business)
end
# Geocoder dependency
def to_coordinates
[latitude, longitude]
end
# Set equality dependencies
def eql?(other_object)
latitude == other_object.latitude && longitude == other_object.longitude
end
def hash
[latitude, longitude].hash
end
endclass DataPoint
attr_reader :latitude, :longitude, :state
def initialize(options)
raise ArgumentError, "Please initialize with :latitude, :longitude"
if options[:latitude].nil? || options[:longitude].nil?
@latitude = options[:latitude].to_f
@longitude = options[:longitude].to_f
@state = options[:state]
end
def geographic_distance(business)
Geocoder::Calculations.distance_between(self, business)
end
# Geocoder dependency
def to_coordinates
[latitude, longitude]
end
# Set equality dependencies
def eql?(other_object)
latitude == other_object.latitude && longitude == other_object.longitude
end
def hash
[latitude, longitude].hash
end
endUp next is the Cluster class, which we will use to perform the following functions:
- Store a centroid and a set of data points.
- Recalculate the position of the centroid to make it equidistant to all points in the cluster within a very small margin of error.
- Implement a method to compare itself with another cluster.
With these specifications in mind, we write the tests:
subject { Algorithms::KMeans::Cluster.new(data_points: [data_point1, data_point2]) }
let(:data_point1) { Algorithms::KMeans::DataPoint.new(latitude: -23.03, longitude: -77.25) }
let(:data_point2) { Algorithms::KMeans::DataPoint.new(latitude: -33.03, longitude: -77.25) }
let(:margin_of_error) { 0.00189394 } #10 ft
describe '#recompute_centroid!' do
it 'sets the centroid to the geographic center of the cluster (within 10ft)' do
subject.recompute_centroid!
new_centroid = subject.centroid
expect(data_point1.geographic_distance(new_centroid))
.to be_within(margin_of_error)
.of(data_point2.geographic_distance(new_centroid))
end
end
describe '#clear!' do
it 'removes all the data points' do
subject.clear!
expect(subject.data_points).to be_empty
end
end
describe '#add_datapoint' do
it 'adds a data point' do
new_data_point = Algorithms::KMeans::DataPoint.new(latitude: -32.32, longitude: 78.2)
expect { subject.add_datapoint(new_data_point) }
.to change { subject.data_points.size }.by(1)
end
end
describe '#==' do
it 'returns true if two clusters have the same data points (order is irrelevant)' do
cluster2 = Algorithms::KMeans::Cluster.new(data_points: [data_point2.dup, data_point1.dup])
expect(cluster2).to be == subject
end
endsubject { Algorithms::KMeans::Cluster.new(data_points: [data_point1, data_point2]) }
let(:data_point1) { Algorithms::KMeans::DataPoint.new(latitude: -23.03, longitude: -77.25) }
let(:data_point2) { Algorithms::KMeans::DataPoint.new(latitude: -33.03, longitude: -77.25) }
let(:margin_of_error) { 0.00189394 } #10 ft
describe '#recompute_centroid!' do
it 'sets the centroid to the geographic center of the cluster (within 10ft)' do
subject.recompute_centroid!
new_centroid = subject.centroid
expect(data_point1.geographic_distance(new_centroid))
.to be_within(margin_of_error)
.of(data_point2.geographic_distance(new_centroid))
end
end
describe '#clear!' do
it 'removes all the data points' do
subject.clear!
expect(subject.data_points).to be_empty
end
end
describe '#add_datapoint' do
it 'adds a data point' do
new_data_point = Algorithms::KMeans::DataPoint.new(latitude: -32.32, longitude: 78.2)
expect { subject.add_datapoint(new_data_point) }
.to change { subject.data_points.size }.by(1)
end
end
describe '#==' do
it 'returns true if two clusters have the same data points (order is irrelevant)' do
cluster2 = Algorithms::KMeans::Cluster.new(data_points: [data_point2.dup, data_point1.dup])
expect(cluster2).to be == subject
end
endFollowed by the class implementation:
class Cluster
require 'geocoder'
attr_reader :data_points, :centroid
def initialize(options)
options = defaults.merge(options)
@data_points = Set.new(options[:data_points])
@centroid = options[:centroid]
end
def recompute_centroid!
lat, lng = Geocoder::Calculations.geographic_center(data_points)
@centroid = DataPoint.new(latitude: lat, longitude: lng)
end
def add_datapoint(data_point)
data_points.add(data_point)
end
def clear!
data_points.clear
end
def ==(other_object)
@data_points == other_object.data_points
end
private
def defaults
{ data_points: Set.new }
end
endclass Cluster
require 'geocoder'
attr_reader :data_points, :centroid
def initialize(options)
options = defaults.merge(options)
@data_points = Set.new(options[:data_points])
@centroid = options[:centroid]
end
def recompute_centroid!
lat, lng = Geocoder::Calculations.geographic_center(data_points)
@centroid = DataPoint.new(latitude: lat, longitude: lng)
end
def add_datapoint(data_point)
data_points.add(data_point)
end
def clear!
data_points.clear
end
def ==(other_object)
@data_points == other_object.data_points
end
private
def defaults
{ data_points: Set.new }
end
endFinally, we implement the algorithm in a class called Clusterer.
This class needs to run through the four steps of the algorithm and
terminate on convergence or after a maximum number of iterations. It
should also export the clustered data in a format that we can plot on a
map. Let's assert these requirements.
let(:filename) { "#{File.dirname(__FILE__)}/../../../fixtures/k_means/data.json" }
subject { Algorithms::KMeans::Clusterer.new(filename: filename) }
let(:east_states) { %w(NY NJ PA MA VA) }
let(:west_states) { %w(CA NV OR WA) }
let(:fly_over_states) { %w(IA MO NE OK SD) }
let(:clusters) do
lat_lngs = [
{ latitude: 37.757717, longitude: -122.410499 }, # San Francisco, CA
{ latitude: 40.764684, longitude: -73.988990 }, # Manhattan, NY
{ latitude: 42.137687, longitude: -100.178348}, # Goose Creek, NE
]
lat_lngs.collect do |ll|
Algorithms::KMeans::Cluster.new(centroid: Algorithms::KMeans::DataPoint.new(ll))
end
end
describe '#run' do
context 'with pre-determined clusters' do
it 'clusters the data into east, west and flyover states' do
subject.clusters = clusters
subject.run
states_by_cluster = subject.clusters.map {|s| s.data_points.classify(&:state).keys.to_set }.to_set
expect(states_by_cluster)
.to eq(Set.new([east_states.to_set, west_states.to_set, fly_over_states.to_set]))
end
end
context 'without pre-determined clusters' do
it 'divides the data into distinct clusters' do
subject.run
expect(subject.clusters.map { |cluster| cluster.data_points.size }.inject(:+))
.to eq(subject.data_points.to_set.size)
end
end
end
describe '#to_chart_data' do
it 'returns an array of data points grouped by cluster' do
subject.clusters = clusters
subject.run
expect(subject.to_chart_data.group_by(&:last).size).to eq(3)
end
endlet(:filename) { "#{File.dirname(__FILE__)}/../../../fixtures/k_means/data.json" }
subject { Algorithms::KMeans::Clusterer.new(filename: filename) }
let(:east_states) { %w(NY NJ PA MA VA) }
let(:west_states) { %w(CA NV OR WA) }
let(:fly_over_states) { %w(IA MO NE OK SD) }
let(:clusters) do
lat_lngs = [
{ latitude: 37.757717, longitude: -122.410499 }, # San Francisco, CA
{ latitude: 40.764684, longitude: -73.988990 }, # Manhattan, NY
{ latitude: 42.137687, longitude: -100.178348}, # Goose Creek, NE
]
lat_lngs.collect do |ll|
Algorithms::KMeans::Cluster.new(centroid: Algorithms::KMeans::DataPoint.new(ll))
end
end
describe '#run' do
context 'with pre-determined clusters' do
it 'clusters the data into east, west and flyover states' do
subject.clusters = clusters
subject.run
states_by_cluster = subject.clusters.map {|s| s.data_points.classify(&:state).keys.to_set }.to_set
expect(states_by_cluster)
.to eq(Set.new([east_states.to_set, west_states.to_set, fly_over_states.to_set]))
end
end
context 'without pre-determined clusters' do
it 'divides the data into distinct clusters' do
subject.run
expect(subject.clusters.map { |cluster| cluster.data_points.size }.inject(:+))
.to eq(subject.data_points.to_set.size)
end
end
end
describe '#to_chart_data' do
it 'returns an array of data points grouped by cluster' do
subject.clusters = clusters
subject.run
expect(subject.to_chart_data.group_by(&:last).size).to eq(3)
end
endHere's an abridged version of the algorithm's implementation, showcasing the meat of the algorithm, which is pretty straightforward. The full Clusterer class is
here.
class Clusterer
MAX_ITERATIONS = 100
def run
load_data_points
compute_initial_centroids if clusters.empty?
MAX_ITERATIONS.times do
clear_clusters
assign_points_to_nearest_cluster
old_clusters = Marshal.load(Marshal.dump(clusters))
recompute_centroids
assign_points_to_nearest_cluster
clusters_did_not_change = old_clusters.zip(clusters).collect {|c1, c2| c1 == c2 }
break unless clusters_did_not_change.include?(false)
end
end
endclass Clusterer
MAX_ITERATIONS = 100
def run
load_data_points
compute_initial_centroids if clusters.empty?
MAX_ITERATIONS.times do
clear_clusters
assign_points_to_nearest_cluster
old_clusters = Marshal.load(Marshal.dump(clusters))
recompute_centroids
assign_points_to_nearest_cluster
clusters_did_not_change = old_clusters.zip(clusters).collect {|c1, c2| c1 == c2 }
break unless clusters_did_not_change.include?(false)
end
end
endResults
Since the k-means algorithm does not guarantee to find the global optimum, we can't expect that the data will be clustered in the same way after each run. However, given that we have some knowledge of the data we are clustering, we can provide initial centroids that will result in the global optimum. For the chart below I picked 500 businesses in groupings of states to make the clustering easier. I also chose the initial centroids to ensure that the algorithm found the global optimum. I plotted the chart using a Google Visualization.
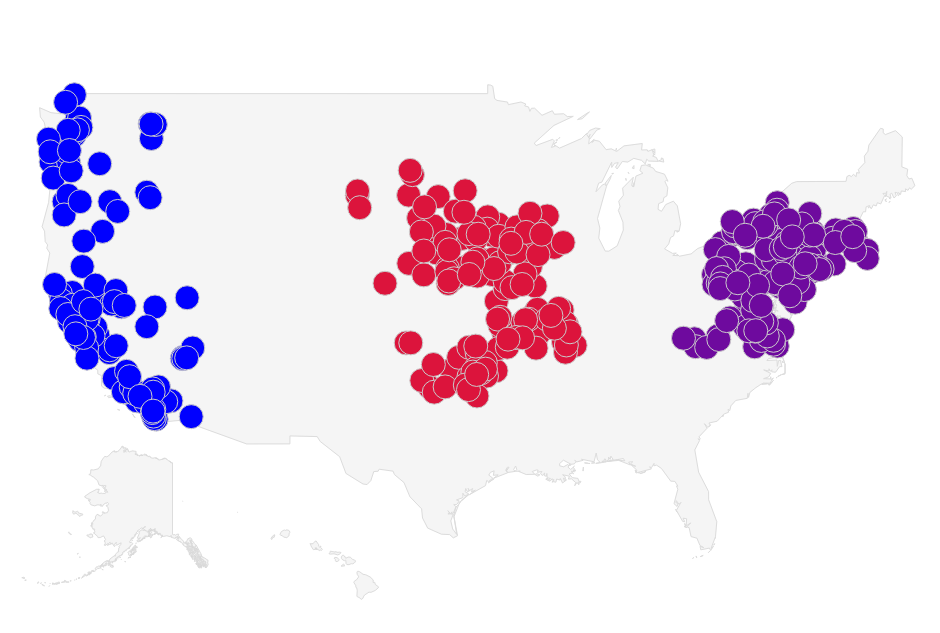
You can find the complete code for this blog post in my algorithms repository on github.